Multi-site, multi-frequency tensor decomposition of magnetotelluric data

Gary W. McNeice*, Phoenix Geophysics Ltd.
Alan G. Jones, Geological Survey of Canada

Summary

Accurate interpretation of magnetotelluric data relies upon an understanding of the directionality and dimensionality inherent in the data, and correct implementation of a method for removing the effects of small-scale galvanic scatterers. The galvanic distortion analysis advocated by Groom and Bailey has become the de facto standard. and rightly so given that the approach both decomposes the magnetotelluric impedance tensor into determinable and indeterminable parts, and tests statistically the validity of the approximation. In its original formulation, one fits the model on a frequency-by-frequency and site-by-site basis independently, and determines qualitatively the most consistent regional strike angle. Whilst this approach has the attraction that one gains a more intimate understanding of the dataset, it is time-consuming and requires repetitive, tedious application. We propose an extension to Groom-Bailey decomposition in which a global minimum is sought for the most appropriate strike direction and distortion parameters for a range of frequencies and a set of sites. We illustrate application of the analysis to synthetic datasets.

Introduction

In recent years, impedance tensor decomposition analysis has become an integral part of modern interpretation of magnetotelluric (MT) data. The objective of this analysis is to remove the first-order effects of galvanic distortion produced by near surface zones of anomalous conductivity, and to recover the impedances and strike of the regional geoelectric structure(s). Of the parameters derived during decomposition analysis, the regional strike is often the poorest resolved parameter (Groom et al. 1993; Jones & Groom 1993), which presents somewhat of a problem, since the accuracy of the interpretation is dependent on the correct adoption of a regional strike consistent with the data. In this GB analysis, galvanic distortion is characterized by two decomposition parameters shear and twist, and induction by the regional strike. These three are iteratively constrained to find frequency-independent estimates required by the decomposition model (see Groom et al. 1993, for a tutorial). Regional strikes determined at each frequency of a set of sites are then compared to obtain an estimate of regional strike for the entire data set (assuming the data are two-dimensional and sensing the same regional 2D structure). For a more representative estimate of regional strike, one really needs to perform a weighted average of the determined strike estimates, since the resolution of regional strike is a function of frequency, site location, and data precision.

In this paper, an extension to Groom-Bailey decomposition is proposed in which the physical constraints implicit to the decomposition model are imposed simultaneously on the data set and a global minimum sought. This procedure enables the determination of the estimate of strike most consistent with the data set in a statistical sense. The variation of strike resolution as a function of frequency and position are used in the determination of the strike estimate. The approach additionally provides the interpreter with information on the degree to which the data fits the model of regional two dimensionality with galvanic distortions.

Synthetic and real data are used to demonstrate the robustness of the proposed decomposition analysis.

Groom-Bailey Decomposition

The basic model is of non-inductive, galvanic distortion by small-scale three-dimensional (3D) bodies in thin surface sheet over a two-dimensional (2D) regional Earth (3D/2D)

(Bahr 1984), where R is a rotation tensor. The elements of the 2x2 tensor C are real and frequency-independent. There have been many approaches proposed to derive the parameters descriptive of the regional conductivity structure; which are the geoelectric strike, , of R, and the two complex impedances of Z_2D. The most appealing to date is the approach of Groom & Bailey (1989), who describe a tensor decomposition based on factoring the telluric distortion tensor C as a product of modified Pauli spin matrices. This allows a separation of determinable and indeterminable elements of the distortion tensor C, as well as providing some physical insight into the distortion produced by elements of the distortion tensor. C is represented by a product factorization

where g is a scalar termed "site gain" and T, S, and A are tensor factors termed twist, shear and anisotropy respectively.

The twist, T, and shear, S, tensors are the determinable parts of the distortion matrix, and the site gain g and anisotropy tensor A form the indeterminable parts.

The seven parameters of the GB factorization are the two descriptors of telluric distortion twist t and shear e, the regional strike , and the four parameters contained in the two complex regional impedances, Z_xy and Z_yx. The parameters of the factorization are found by statistically fitting the seven parameters of the decomposition model to the eight (8) data of the measured impedance tensor.

In formal GB analysis the decomposition model is fit to the measured data frequency by frequency and site by site. However, for the 3D/2D distortion model to be valid frequency independent estimates of the twist, shear and regional strike must be found over a band of frequencies and a group of neighbouring sites. In practice this is done by iteratively constraining the estimates of twist, shear and strike found at each frequency in an attempt to find a frequency band for which the constrained values result in an acceptable misfit error (Groom et al. 1993). If the regional conductivity structure is truly 1D or 2D, the model will hold in general at low frequencies reducing the task to finding an upper frequency limit below which the distortion becomes solely galvanic (distorter becomes inductively small) and the distortion parameters become frequency independent.

Regional strike estimation

Of the parameters solved for in decomposition analysis of the impedance tensor, regional strike is by far the most important parameter. Accurate recovery of the regional impedances, and therefore accuracy of the interpretation, is dependent on recovery of the correct regional strike. Unfortunately, regional strike is often one of the poorest resolved parameters in decomposition analysis (Jones & Groom 1993). The resolution of regional strike is a function of both frequency and position and its recovery is impeded by galvanic distortion and experimental error.

The importance of accurate recovery of the regional strike can be seen by examining properties of the measured impedance tensor under Groom-Bailey factorization. In an arbitrary coordinate system, the measured impedance tensor is given by (1). The elements of the impedance tensor are distortion and rotation dependent mixtures of the two regional impedances. In the regional coordinate system however, (1) reduces to

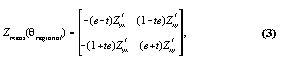and the two columns of the impedance tensor contain scaled estimates of the regional impedances (denoted by the prime). The impedance elements contained in the two columns are linearly dependent, having the same impedance phase, differing solely in magnitude. This phase relationship was first recognized by Bahr (1984). The magnitude of the four elements is described by the twist (t) and shear (e) factors of the GB factorization.

Equation (3) shows that theoretically scaled estimates of the regional impedances can be found in the presence of galvanic distortion by simply rotating the impedance tensor to the regional coordinate system. An error in the regional strike estimate will results in the recovery of impedances which are mixtures of the regional impedances, while errors in twist and shear result solely in errors in the magnitudes of the recovered regional impedances. Recovery of the correct regional strike is therefore essential for accurate recovery of the regional impedances.

In the decomposition procedures proposed by Zhang et al. (1987), Bahr (1988), Chakridi et al. (1992), and Smith (1995) the linear dependence of the columns of the impedance tensor is used to find the regional strike. Their procedures solve for a strike angle for which the elements of the two columns have equal impedance phases. This method however is unstable in the presence of noise since depending on distortion (twist and shear) some of the elements of the tensor can be small in magnitude and dominated by error, producing significant errors in the recovered regional strike (Jones & Groom 1993).

Groom-Bailey decomposition performs better in the presence of noise since it simultaneously solves for all of the parameters of the decomposition model. Twist and shear are often better resolved than the regional strike as they are dependent on the relative magnitude of the impedance elements as opposed to phase properties of the elements. The inclusion of twist and shear into a model fitting all eight elements of the impedance tensor stabilizes the estimation of regional strike.

Extension of Groom-Bailey Decomposition for Multiple Sites and Multiple Frequencies

To improve the estimation of regional strike, one can extend the GB analysis to fit statistically an entire dataset simultaneously with the assumed 3D/2D distortion model. The regional strike is usually only well defined over a small subset of the data., and thus this extension yields superior strike estimation since it accounts for the position and frequency dependence of strike resolution. The dependence of model misfit on strike defines a regional strike statistically consistent with the entire data set.

In the extended GB analysis, S magnetotelluric sites having N frequencies (S*N*8 data, for data at every frequency from every site) can be fit with S*(N*4 + 2) + 1 unknowns. The unknowns are the S*N regional complex impedances (Z_xy and Z_yx), the S*2 descriptors of telluric distortion (twist t and shear e) and the regional strike angle (). In the extended model the S sites are required to have the same regional strike; the telluric distortion parameters shear and twist remain site dependent although independent of frequency. Assuming that all the data are independent, the model has S*(N*4 - 2) - 1 degrees of freedom. In the case of a single site, the extended model is equivalent to that of the GB method with the strike, twist and shear constrained to be independent of frequency, although the solutions are arrived at differently.

The model parameters are found in the extended analysis by minimizing a misfit function based on the observed and model summary decomposition coefficients. The elements of each of the modelled impedance tensors are described by four complex nonlinear equations, and the minimization procedure seeks a simultaneous solution to the S*N*8 nonlinear equations (4 real and 4 imaginary equations for each of the S*N impedance tensors) describing the measured data set. An objective functional normalized by the data variances was chosen in order to reduce any bias produced by frequency and position dependence of experimental error and the frequency dependence of impedance magnitudes. Additionally, the objective function allows one to derive significance levels for the parameter estimates obtained by the minimization procedure.

Errors on the parameters are derived using a bootstrap method similar to that of Groom & Bailey (1991).

Failure of decomposition analysis

There are two situations that can occur in decomposition analysis of the impedance tensor, where the method fails to recover the regional impedances accurately. Decomposition fails when the shear approaches 45⁰ (e of 1) or when the sum of distortion and regional anisotropy approaches an s of 1. In both situations, decomposition analysis fails because the measured impedance tensor approaches singularity and the decomposition model becomes underdetermined.

In the case of high shear the two rows of the impedance tensor become linearly dependent in any coordinate system. The strike therefore is unresolvable, as the impedance tensor assumes the form of a distorted 2D tensor in any coordinate system. The shear angle will be well resolved by the linear dependence of the two rows, although only the sum of the regional strike and twist angles will be resolved. In order to recover the regional impedances the strike must be found from adjacent sites or other independent information.

In the high anisotropy case, the distortion parameters cannot be resolved and while a strike angle is resolved, it cannot be determined if it is that of the regional structure or a local distorter. If the strike determined by decomposition is in agreement with the regional strike found at other nearby sites (in an inductive sense) it may be reasonable to assume that the recovered impedances are those of the regional structure.

Examples of Application

Synthetic Example I

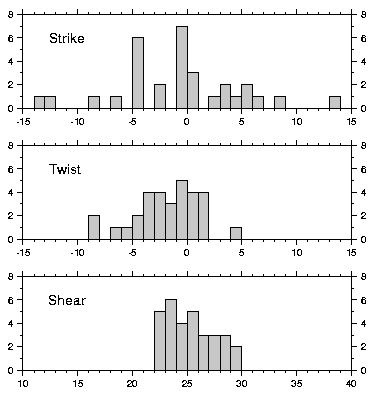
To illustrate the performance of the proposed decomposition procedure in the presence of experimental noise, thirty-one realizations of the theoretical impedance tensor discussed by Jones & Groom (1993) were generated. The distorted tensor has a site gain (g) of 1.06, an anisotropy (s) of 0.172, a twist angle of -2.1 (t = -0.037), and a shear angle of 24.95 (e = 0.47). The inductive 2D regional strike is 0.

Gaussian noise, having a standard deviation of 4.5% of the magnitude of the largest impedance element, was added to the tensor (4) to produce thirty-one noise-contaminated realizations. These thirty-one realizations form an ideal data set to test the performance of the decomposition procedure in the presence of noise, as all the realizations are equally sensitive to the inductive strike and obey the telluric distortion model differing solely by experimental noise.

Figure 1 shows histograms of the strike, twist and shear found from an unconstrained GB analysis of the thirty-one realizations. The distributions of the GB parameters clear shows that shear and twist are more stable under decomposition than strike angle determination. The strike directions determined appear to be approximately normally distributed, although they ill define the regional strike.

The results of the extended decomposition analysis yields a twist angle of -2.2, a shear angle of 25.6 and strike direction of 0.1, very close to the correct values of -2.1, 24.95 and 0 respectively. The results appear to be accurate and free of noise bias, in contrast to the outcome of iteratively constraining the frequency-dependent decomposition parameters as advocated by Groom et al. (1993). Such a procedure resulted in an estimate of strike of -7 4 (Jones & Groom 1993).

Synthetic Example II

Now we evaluate decomposition analysis of a more realistic theoretical response, where sensitivity to the 2D inductive strike is a function of frequency. Groom & Bailey (1991) produced an accurate 3D/2D dataset by superposing 2D numerical and 3D analytic responses. The 3D analytical response is that of a small conducting hemisphere, and the 2D host is a fault-like structure. For the frequencies considered the hemisphere has a negligible inductive response, but it has a significant effect on both the electric and magnetic fields of the regional 2D structure. For frequencies <10 Hz (periods >0.1 s), the distortion effects produced by the anomalous magnetic fields of the hemisphere become negligible and the hemisphere acts as a galvanic scatterer.

The strike of the regional 2D structure is 30. Groom et al. (1993) have shown that the strike is poorly defined at both short and long periods. For short periods the data are insensitive to the 2D boundaries of the regional structure and are essentially 1D, whereas at long periods the 2D structure becomes inductively thin, having only a galvanic response which combines with the galvanic response of the hemispherical distorter. The phases of the two regional impedances become virtually identical, and the regional response becomes an anisotropic 1D response (2D galvanic distortion of the response of the deep regional 1D structure).

To simulate experimental noise, 2% Gaussian noise was added to the theoretical responses. Decomposition analysis, prior to the addition of noise, yields a twist angle of -12 and shear angle of 30 (Groom et al. 1993). The 3D scattering effects of the hemisphere in this data set are first-order effects while the inductive response of the 2D structure has a much smaller effect, making this a good dataset for testing the extended decomposition routine.

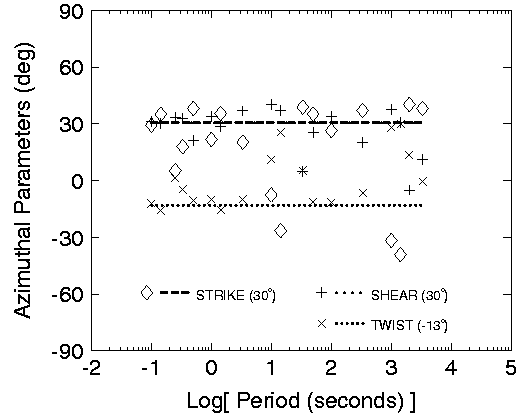The results of the extended decomposition analysis are shown superimposed on the results of the unconstrained GB analysis in Fig 2. The extended analysis yields a strike direction of 30.7, twist angle of -13.0 and shear of 30.6. The extended model has 69 degrees of freedom, with a 95% confidence level having a ² value of 90.0. The chi-squared misfit of the model is 49.5, well below the 95% confidence level.

The extended analysis recovers each of the regional responses to within a multiplicative static shift factor. The magnitude and phase of the Z_yx (TM mode) impedance are contaminated by noise at long periods where the Z_yx impedance is small in magnitude. This noise contamination is enhanced by the distortion anisotropy, which reduces the magnitude of the Z_yx impedance. However, the long period Z_yx impedances would have the highest scatter even in the absence of distortion due to their small magnitude.

Conclusions

We have extended the Groom-Bailey decomposition method to find the most consistent 2D parameters from a set of sites over a given frequency band. This method allows one to determine rapidly a regional strike statistically consistent with frequency, site location and data precision dependencies. The recovered impedances, where the 3D/2D decomposition model holds, are free of first-order effects of galvanic distortion, and the procedure provides a validation for further 2D interpretation. However, we advocate careful use of this global minimization, as the parameters may vary with frequency as, for example, the strike may be depth-dependent (see, e.g., Marquis et al., 1995).

References

Bahr, K. 1984. Elimination of local 3D distortion of the magnetotelluric tensor impedance allowing for two different phases. Contributed paper at Seventh Workshop on Electromagnetic Induction in the Earth and Moon, held in Ile-Ife, Nigeria, August 15-22.

Bahr, K. 1988. Interpretation of the magnetotelluric impedance tensor, regional induction and local telluric distortion. J. Geophys., 62, 119-127.

Bahr, K. 1991. Geologic noise in magnetotelluric data: a classification of distortion type. Phys. Earth. Planet. Inter., 66, 24-38.

Chakridi, R., Chouteau, M. & Mareschal, M. 1992. A simple technique for analysing and partly removing galvanic distortion from the magnetotelluric impedance tensor: application to Abitibi and Kapuskasing data (Canada). Geophys. J. Inter., 108, 917-929.

Groom, R.W. & Bailey, R.C. 1989. Decomposition of magnettotelluric impedance tensors in the presence of local three-dimensional galvanic distortion. J. Geophys. Res., 94, 1913-1925.

Groom, R.W. & Bailey, R.C. 1991. Analytic investigations of the effects of near-surface three-dimensional galvanic scatters on MT tensor decompositions. Geophysics, 56, 496-518.

Groom, R.W., Kurtz, R.D., Jones, A.G. & Boerner, D.E., 1993. A quantitative methodology for determining the dimensionality of conductivity structure and the extraction of regional impedance responses from magnetotelluric data. Geophys. J. Inter, 115, 1095-1118.

Jones, A.G. & Groom, R.G. 1993. Strike angle determination from the magnetotelluric impedance tensor in the presence of noise and local distortion: rotate at your peril! Geophys. J. Inter., 113, 524-534.

Marquis, G., Jones, A.G. & Hyndman, R.D., 1995. Coincident conductive and reflective lower crust across a thermal boundary in southern British Columbia, Canada. Geophys. J. Int., 20, 111-131.

Smith, J.T., 1995, Understanding telluric distortion matrices. Geophys. J. Int., 122, 219-226.

Zhang, P., Roberts, R.G. & Pedersen, L.B. 1987. Magnetotelluric strike rules. Geophysics, 52, 267-278.